Detectores Espectrales y de Continuo
Generalidades sobre back-ends
Se denomina back-end al conjunto de subsistemas situados al final de la cadena receptora, encargados del tratamiento de la señal recibida previamente detectada y convertida a frecuencia intermedia en el front-end (que llamaremos señal de FI). Existen distintos tipos de back-end:
- Los que sólo registran la señal de FI con un determinado formato e información adicional de la observación para su posterior tratamiento y análisis, como es el caso de los backend de VLBI (por ejemplo, el Mark IV).
- Los que la detectan y procesan. Estos últimos se dividen a su vez en dos tipos, Continuo y Espectral, según la forma de detección de la señal de FI:
- El detector de continuo estima la potencia recibida en toda la banda de paso del receptor.
- El detector espectral, también llamado espectrómetro, estima la densidad espectral de potencia, DEP, de la señal de FI dividiendo la banda de paso del receptor en tramos adyacentes y midiendo la potencia recibida en cada tramo. Esto permite, por ejemplo, estudiar las líneas de emisión de los átomos y moléculas del medio interestelar.
El espectrómetro es probablemente el back-end de propósito general más importante en un radiotelescopio. Sus características más importantes son:
- El ancho de banda de la señal de FI que puede analizar.
- La resolución espectral de la DEP (esto es, el grado de detalle de los espectros obtenidos).
- La flexibilidad para elegir los parámetros anteriores.
Hay tres tipos fundamentales de espectrómetros radio: el banco de filtros, el espectrómetro acusto-óptico y el autocorrelador digital.
Banco de filtros
Divide la banda de FI en N subbandas consecutivas, con un banco de N filtros de frecuencias de corte adyacentes de forma que, a la salida de cada filtro, se detecta la potencia que llega en esa subbanda usando un detector cuadrático.
Para que funcione correctamente la función de transferencia de los N filtros debe ser idéntica. Además será necesario realizar ciclos de calibración periódicos para eliminar las variaciones de ganancia entre subbandas debido a que es imposible que los componentes electrónicos de cada subbanda tengan exactamente el mismo comportamiento.
En este espectrómetro el coste por canal es elevado aunque su inconveniente fundamental es que no permite variar la resolución. La resolución máxima es la anchura del filtro y para modificarla habría que cambiar los filtros. Por esta razón, este tipo de espectrómetro es poco utilizado en la actualidad.
Espectrómetro acusto-óptico
Se basa en la difracción que experimenta un haz de luz monocromática al atravesar un líquido sometido a una onda ultrasónica, efecto predicho en 1921 por Brillouin. La señal de FI se convierte en una onda ultrasónica (haciendo uso de un transductor piezoeléctrico) que atraviesa un medio (habitualmente un líquido transparente). Esa onda produce variaciones periódicas de la densidad de dicho medio, lo que a su vez causa variaciones del índice de refracción del medio, a un ritmo mucho menor que la velocidad de la luz por lo que pueden considerarse estacionarias. En estas condiciones, un haz de luz monocromática que atraviese dicho medio será difractado en una dirección que depende de la distancia entre puntos de máxima densidad, lo que significa que el ángulo de difracción del haz depende de la frecuencia de la señal de FI. La cantidad de luz difractada en cada ángulo está directamente relacionada con la potencia de cada frecuencia de la señal de FI.
Las ventajas de este espectrómetro es que permite analizar grandes anchos de banda, con un gran número de canales por banda y un bajo coste por canal. Sin embargo, mecánicamente son delicados, la máxima resolución alcanzable es menor que la del autocorrelador digital, no permite variar la resolución y hay que someterlo a calibraciones periódicas.
Autocorrelador digital
Es un espectrómetro digital que estima el espectro de potencia de la señal de FI haciendo uso del teorema de Wiener-Kintchine, que relaciona la DEP de un proceso aleatorio ergódico y la transformada de Fourier de su función de autocorrelación, ACF.
En concreto se llama autocorrelador digital al circuito que estima la ACF de la señal de FI, para lo cual primero ha de convertirse la señal de FI, analógica, en una señal análoga pero digital. Este proceso consta de dos partes, el muestreo y la cuantificación. Las funciones que realiza el autocorrelador son las siguientes:
Muestrea la señal de FI cumpliendo el teorema de Nyquist. La máxima frecuencia de muestreo que pueda implementarse limita el ancho de banda de la señal de FI.
Cuantificación de las muestras: Consiste en asignar un valor numérico discreto a cada intervalo continuo de amplitudes de las muestras de la señal de FI. Para dos niveles de cuantificación, lo que equivale a especificar la amplitud de la muestra con 1 bit (esto es, sólo se recoge la información del signo de la amplitud de la muestra), se produce una degradación de la sensibilidad del radiómetro de 1.9dB (36%).
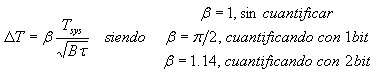
Usando 2-bit (cuatro niveles de cuantificación) y eligiendo un valor óptimo del umbral de amplitud, la cuantificación produce una degradación de la sensibilidad de tan solo 0.5dB (12%), con un aumento asumible de la complejidad del autocorrelador.
Se retardan las muestras y se multiplican adecuadamente, para obtener la estimación de la ACF de la señal de FI digitalizada:
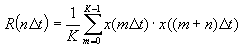
donde n = 0,1,..N-1 siendo N el número máximo de retardos del autocorrelador (o número de canales), K el número de productos promediados y Dt el periodo de muestreo, que limita el máximo ancho de banda de la señal de FI que podremos analizar con el autocorrelador.
La ACF así obtenida es sólo una estimación debido a que:
- K, el número de productos promediados, es un número finito lo que significa que se calcula la ACF sólo de un tramo de la señal de FI.
- N, el número de retardos del autocorrelador, es finito. Esto es, no se calcula la ACF completa, sino sólo un tramo de N valores y,por tanto, la DEP (calculada como la transformada de Fourier de la ACF), tendrá también N valores. Calcular sólo N valores de ACF equivale, en el dominio del tiempo, a multiplicar la ACF completa por una ventana rectangular, y en el dominio de la frecuencia, a convolucionar la transformada de Fourier de la ACF completa, que sería la DEP real, con la transformada de Fourier de la ventana. Esta convolución limita la resolución de la DEP (mínima separación entre canales). Se puede concluir que, cuanto mayor sea el número de canales o retardos del autocorrelador, mayor será la resolución de la DEP resultante.
- El proceso de cuantificación introduce un término de error que puede reducirse aplicando el teorema de Van Vleck.
Después, un microprocesador realiza básicamente las siguientes operaciones:
- Normaliza la ACF calculada en el correlador, para poder aplicar la corrección del teorema de Van Vleck.
- Aplica la corrección de Van Vleck, que establece la relación que existe entre la ACF calculada a partir de la señal de FI cuantificada (con 1 o 2 bits) y la ACF calculada a partir de la señal de FI sin cuantificar. Este teorema es aplicable ya que la señal de FI es de estadística gaussiana.
- Se enventana la ACF con una ventana apropiada. Como hemos dicho anteriormente, tomar sólo un número N de muestras de la ACF equivale a aplicar una ventana cuadrada sobre la ACF completa. Esto produce un suavizado de la DEP al quedar convolucionada con la transformada de Fourier de la ventana rectangular, cuya forma en frecuencia se representa con la función sinc. Aplicando otro tipo de ventanas, como la de Hanning, se puede conseguir disminuir el efecto de los altos lóbulos secundarios de la ventana principal de la sinc, y por consiguiente, un ligero empeoramiento de la resolución del autocorrelador.
- Cálculo de la transformada de Fourier de la ACF enventanada. Habitualmente se calcula la FFT (Fast Fourier Transform) para lo cual es necesario que el número de muestras de la ACF, N, sea potencia de 2.
- Se calibra el espectro obtenido mediante una medida de calibración independiente, con una carga caliente.
Existen dos arquitecturas para construir un autocorrelador, la XF y la FX. La diferencia entre ambas es el orden en que se realizan las operaciones "cálculo de la ACF" y "transformada de Fourier":
- La arquitectura del autocorrelador se denomina XF cuando se calcula primero la función de autocorrelación (de la señal de entrada) y después la transformada de Fourier de la función de autocorrelación. No requieren realizar la transformada de Fourier (FFT) en tiempo real. Se utiliza cuando el número de antenas (señales a correlar) es pequeño puesto que la complejidad (y por tanto el coste de fabricación) del autocorrelador digital aumenta con el cuadrado del número de antenas.
- Se llama arquitectura FX cuando se calcula primero la transformada de Fourier de la señal de FI muestreada y luego la autocorrelación (que equivale a multiplicar la transformada por la transformada de Fourier conjugada y dividir por T). Se utiliza en interferómetros cuando el número de antenas es grande porque resulta más barato ya que, al aumentar el número de antenas, el aumento de la complejidad es lineal. El inconveniente es que requieren procesadores FFT en tiempo real.
El autocorrelador digital es el espectrómetro más utilizado en la actualidad debido a que permite variar la resolución espectral, tiene gran estabilidad en frecuencia al enganchar todos los osciladores a un patrón común (MASER) y su coste es bajo.
Back-ends en el CAY
Existen cuatro tipos de back-end actualmente en funcionamiento:
- Detector de continuo: 50MHz - 1500MHz
- Banco de filtros:
Número de canales 256 Resolución 50 kHz - Espectrómetro acusto-óptico:
Número de canales 576 Resolución 108 kHz - Back-end para VLBI
Terminal VLBA 4 (VLBA DAR y formateador Mark 4)
Dos registradores:
- En cinta magnética de alta densidad (estándar Mark4).
- En paquetes de discos duros (estándar Mark 5).
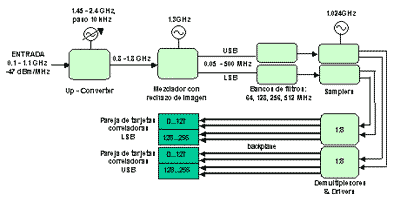
Actualmente se está desarrollando en el CAY un espectrómetro autocorrelador digital de 2 bit/muestra y arquitectura XF para el Radiotelescopio de 40m. A continuación se muestra un esquema general y un resumen de sus parámetros principales:
| Ancho de banda (MHz) | Resolución (kHz) |
| 1024 | 2000 |
| 512 | 500 |
| 256 | 125 |
| 128 | 62.5 |